
Ley Line Physics
Ley Line Physics
English: lots of stuff can chuck out a ley line
Jargon: combinations of mineral and water can emit energy, such as blackband ironstone below chalk and flint
English: mind-bogglingly tiny particles do not move in straight lines, they move in waves, just like radio and sound
Jargon: any quanta below the Planck Length traverse a waveform path
English: you most often find ley lines as a group of seven parallel dowsing lines, with the central line going through an ancient monument
Jargon: static waveform emissions from below ground often emerge at the surface as seven parallel bands of coherent phase output, with the central primary band passing through the main axis of an ancient feature, such as Jacob’s Barrow also known as Golden Cross
English: you can get all techie and tell the energy frequency by measuring the width of the central line
Jargon: energy emission frequency = waveform propagation speed / wavelength
At Jacob’s Barrow, the central primary band is 30cm wide, so the frequency is about 1 GigaHertz, which is 299,000,000 / 0.3
English: it might not be radio, it could be something else
Jargon: although electromagnetic emissions are a candidate, other types of quanta might produce a dowsing reaction, so for example, it could be a lepton signal
Acknowledgements: my thanks to Professor Jim Al-Khalili, Nuclear Physics quantum emissions expert at Surrey University, for pointing out the wide range of candidate quanta that might be responsible.
English: you can tell how deep the ley line is if there are no underground reflections from things like clay
Jargon: strata composition can cause reflections, but in favourable locations like Jacob’s Barrow, you can simply use pythagorean geometry and trigonometry to determine the signal origin depth
Acknowledgements: my thanks to Laurie Booth of The British Society of Dowsers, for pointing out that dowsing reflections are extremely common, from layers of clay for example, thus making Jacob’s Barrow a site with rare clarity of output. Luckily, the maths works so precisely that there is little scope for alternative explanations.
English: when you find seven parallel lines spread over about 60 metres, you’ve got a ley line
Jargon: the waveform emission angle repeats, often in the range 23 to 26 degrees, resulting in seven parallel lines, where the three central lines are close together, with the tertiary pair being further out and the quaternary pair being at the outer limit of the effect. Drought conditions at Jacob’s Barrow gives 5.1m from central primary line to each secondary parallel line, 12.4m from primary to tertiary and 31.3m from primary to quaternary. These are widths W1, W1+W2 and W1+W2+W3.
English: you need to do trig to prove you’ve got a ley line
Jargon: right-angle triangles are used to check site measurements, since at the signal origin depth, distance from primary to another parallel / tangent of angle multiple is constant, so the general formula is
tangent of repeating angle = width from primary to target parallel line
For the parallel lines at Jacob’s Barrow, in drought conditions:
23 degrees is the angle to secondary parallel line and tan 23 = 0.4244748
46 degrees (23 x 2) is the angle to tertiary parallel line and tan 46 = 1.0355303
69 degrees (23 x 3) is the angle to quaternary parallel line and tan 69 = 2.6050891
so W1 / (repeating angle) should equal (W1+W2) / 2(repeating angle)
W1 / tan 23 should equal (W1+W2) / tan 46
5.1m / 0.4244748 should equal 12.4m / 1.0355303
12.014847m should equal 11.97454m, which is the signal origin depth below the ground,
which is 12m down, with slight inequality of 0.040307m (about 4cm) due to only dealing in whole degrees
check this still works with the quaternary parallel line
23 degrees x 3 is 69 degrees for the angle to the fourth parallel
tan 69 degrees = 2.6050891 = W1+W2+W3 / signal origin depth
so 2.6050891 X 12m = 31.26m from primary to quaternary parallel line
which agrees with actual measurements of W1 = 5.1, W2 = 7.3 and W3 = 18.9
where W3 is only 0.04m (again, about 4cm) adrift
so all the maths works, confirming we have a genuine example of an energy emission ley-line.
By Martin Straw 27th March 2009.
Updated by Martin Straw:
1st May 2009
5th May 2009

Jacob’s Barrow, also called Golden Cross, in the New Forest, close to the B3080 and the village of Hale, SU 213 179, archaeology UID 19860.
Summer photograph.

Jacob’s Barrow, also called Golden Cross, next to the B3080 in the New Forest, close to the village of Hale, SU 213 179, archaeology UID 19860.
Winter photograph.

Jacob’s Barrow, also named Golden Cross. Active ley-line earth emissions diagram and maths, at SU 213 179, archaeology UID 19860.
Drought conditions, when signal origin depth has sunk to 12 metres below ground.
Energy emission frequency approx 1GHz.
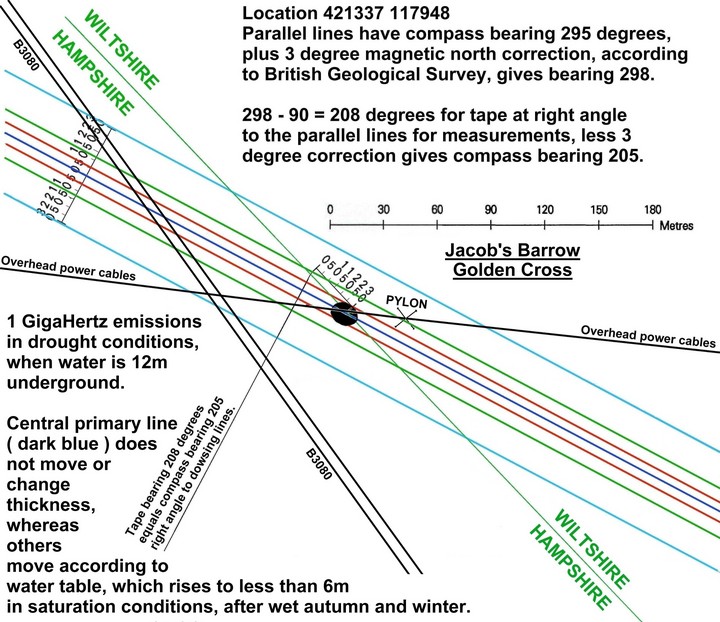
Parallel 1Ghz energy emission lines at Jacob’s Barrow, AKA Golden Cross, under drought conditions. All lines emit the same frequency, defined by the central primary line, which is always 0.3m wide, regardless of weather.
Sorry about this (possibly dim) question. You have stated that ley-lines can be discerned from, for example, energy emitted by combinations of mineral and water and that ancient monuments are often placed on the central line. Doesn't this make it unlikely, given the meandering underground , that ley-lines would match up with straight lines of monuments across the landscape?
Yes indeed Gjrk, this is where the straight lines of blackbank ironstone come into play, so this type of situation is probably rare. Whilst many ley-lines are merely visual alignments, earth-energy ideas are not all fiction. Jacob's Barrow is oval, implying some kind of orientation or bearing, whilst the primary (central) energy line dowses right through the central axis of the oval. In drought conditions, the pair of secondary parallel lines mark the outer edge of the mound, but in wetter seasons, the water table rises, causing all seven parallel lines to appear to be closer togther, because the signal origin depth has risen from 12 metres to less than 6 metres below the surface. At this location, the lines are straight for at least 60 metres either side of the barrow. Thanks for your interest.
No problem. Thanks for the information :)